Units of Measurement

Quanta

Quanta, Units, and Conversions

UnittedQuantity is the primary case class in axle.quanta

The axle.quanta package models units of measurement. Via typeclasses, it implements expected operators like +, -, a unit conversion operator in, and a right associative value constructor *:

The "quanta" are Acceleration, Area, Angle, Distance, Energy, Flow, Force, Frequency, Information, Mass, Money, MoneyFlow, MoneyPerForce, Power, Speed, Temperature, Time, and Volume. Axle's values are represented in such a way that a value's "quantum" is present in the type, meaning that nonsensical expressions like mile + gram can be rejected at compile time.

Additionally, various values within the Quantum objects are imported. This package uses the definition of "Quantum" as "something that can be quantified or measured".

import axle._
import axle.quanta._
import axle.jung._

Quanta each define a Wikipedia link where you can find out more about relative scale:

Distance().wikipediaUrl
// res0: String = "http://en.wikipedia.org/wiki/Orders_of_magnitude_(length)"

A visualization of the Units of Measurement for a given Quantum can be produced by first creating the converter:

import edu.uci.ics.jung.graph.DirectedSparseGraph
import cats.implicits._
import spire.algebra.Field
import axle.algebra.modules.doubleRationalModule

implicit val fieldDouble: Field[Double] = spire.implicits.DoubleAlgebra
implicit val distanceConverter = Distance.converterGraphK2[Double, DirectedSparseGraph]

Create a DirectedGraph visualization for it.

import cats.Show

implicit val showDDAt1 = new Show[Double => Double] {
  def show(f: Double => Double): String = f(1d).toString
}

import axle.visualize._

val dgVis =
  DirectedGraphVisualization[
    DirectedSparseGraph[UnitOfMeasurement[Distance],Double => Double],
    UnitOfMeasurement[Distance], Double => Double](distanceConverter.conversionGraph)

Render to an SVG.

import axle.web._
import cats.effect._

dgVis.svg[IO]("docwork/images/Distance.svg").unsafeRunSync()

Distance conversions

Units

A conversion graph must be created with type parameters specifying the numeric type to be used in unitted quantity, as well as a directed graph type that will store the conversion graph. The conversion graphs should be placed in implicit scope. Within each are defined units of measurement which can be imported.

implicit val massConverter = Mass.converterGraphK2[Double, DirectedSparseGraph]
import massConverter._

implicit val powerConverter = Power.converterGraphK2[Double, DirectedSparseGraph]
import powerConverter._

import axle.algebra.modules.doubleRationalModule

// reuse distanceConverter defined in preceding section
import distanceConverter._

implicit val timeConverter = Time.converterGraphK2[Double, DirectedSparseGraph]
import timeConverter._

Standard Units of Measurement are defined:

gram
// res2: UnitOfMeasurement[Mass] = UnitOfMeasurement(
//   name = "gram",
//   symbol = "g",
//   wikipediaUrl = None
// )

foot
// res3: UnitOfMeasurement[Distance] = UnitOfMeasurement(
//   name = "foot",
//   symbol = "ft",
//   wikipediaUrl = None
// )

meter
// res4: UnitOfMeasurement[Distance] = UnitOfMeasurement(
//   name = "meter",
//   symbol = "m",
//   wikipediaUrl = None
// )

Construction

Values with units are constructed with the right-associative *: method on any spire Number type as long as a spire Field is implicitly available.

10d *: gram

3d *: lightyear

5d *: horsepower

3.14 *: second

200d *: watt

Show

A witness for the cats.Show typeclass is defined. show will return a String representation.

import cats.implicits._

(10d *: gram).show
// res10: String = "10.0 g"

Conversion

A Quantum defines a directed graph, where the UnitsOfMeasurement are the vertices, and the Conversions define the directed edges. See Graph Theory for more on how graphs work.

Quantities can be converted into other units of measurement. This is possible as long as 1) the values are in the same Quantum, and 2) there is a path in the Quantum between the two.

(10d *: gram in kilogram).show
// res11: String = "0.010000000000000002 Kg"

Converting between quanta is not allowed, and is caught at compile time:

(1 *: gram) in mile
// error: type mismatch;
//  found   : axle.quanta.UnitOfMeasurement[axle.quanta.Distance]
//  required: axle.quanta.UnitOfMeasurement[axle.quanta.Mass]
// (1 *: gram) in mile
//                ^^^^

Math

Addition and subtraction are defined on Quantity by converting the right Quantity to the unit of the left.

import spire.implicits.additiveGroupOps

((7d *: mile) - (123d *: foot)).show
// res13: String = "36837.0 ft"
{
  import spire.implicits._
  ((1d *: kilogram) + (10d *: gram)).show
}
// res14: String = "1010.0 g"

Addition and subtraction between different quanta is rejected at compile time:

(1d *: gram) + (2d *: foot)
// error: type mismatch;
//  found   : String
//  required: Int
//   ((1d *: kilogram) + (10d *: gram)).show
//   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
// error: type mismatch;
//  found   : axle.quanta.UnittedQuantity[axle.quanta.Distance,Double]
//  required: String
// (1d *: gram) + (2d *: foot)
//                    ^^^^^^^

Scalar multiplication comes from Spire's CModule typeclass:

import spire.implicits.rightModuleOps

((5.4 *: second) :* 100d).show
// res16: String = "540.0 s"
((32d *: century) :* (1d/3)).show
// res17: String = "10.666666666666666 century"

Unitted Trigonometry

Versions of the trigonometric functions sine, cosine, and tangent, require that the arguments are Angles.

Preamble

Imports, implicits, etc

import edu.uci.ics.jung.graph.DirectedSparseGraph

import cats.implicits._

import spire.algebra.Field
import spire.algebra.Trig

import axle.math._
import axle.quanta.Angle
import axle.quanta.UnitOfMeasurement
import axle.algebra.modules.doubleRationalModule
import axle.jung.directedGraphJung

implicit val fieldDouble: Field[Double] = spire.implicits.DoubleAlgebra
implicit val trigDouble: Trig[Double] = spire.implicits.DoubleAlgebra

implicit val angleConverter = Angle.converterGraphK2[Double, DirectedSparseGraph]

import angleConverter.degree
import angleConverter.radian

Examples

cosine(10d *: degree)
// res19: Double = 0.984807753012208

sine(3d *: radian)
// res20: Double = 0.1411200080598672

tangent(40d *: degree)
// res21: Double = 0.8390996311772799

Geo Coordinates

Imports and implicits

import edu.uci.ics.jung.graph.DirectedSparseGraph

import cats.implicits._

import spire.algebra.Field
import spire.algebra.Trig
import spire.algebra.NRoot

import axle._
import axle.quanta._
import axle.algebra.GeoCoordinates
import axle.jung.directedGraphJung
import axle.algebra.modules.doubleRationalModule

implicit val fieldDouble: Field[Double] = spire.implicits.DoubleAlgebra
implicit val trigDouble: Trig[Double] = spire.implicits.DoubleAlgebra
implicit val nrootDouble: NRoot[Double] = spire.implicits.DoubleAlgebra

implicit val angleConverter = Angle.converterGraphK2[Double, DirectedSparseGraph]
import angleConverter.°

Locations of SFO and HEL airports:

val sfo = GeoCoordinates(37.6189 *: °, 122.3750 *: °)
sfo.show
// res23: String = "37.6189° N 122.375° W"
val hel = GeoCoordinates(60.3172 *: °, -24.9633 *: °)
hel.show
// res24: String = "60.3172° N -24.9633° W"

Import the LengthSpace

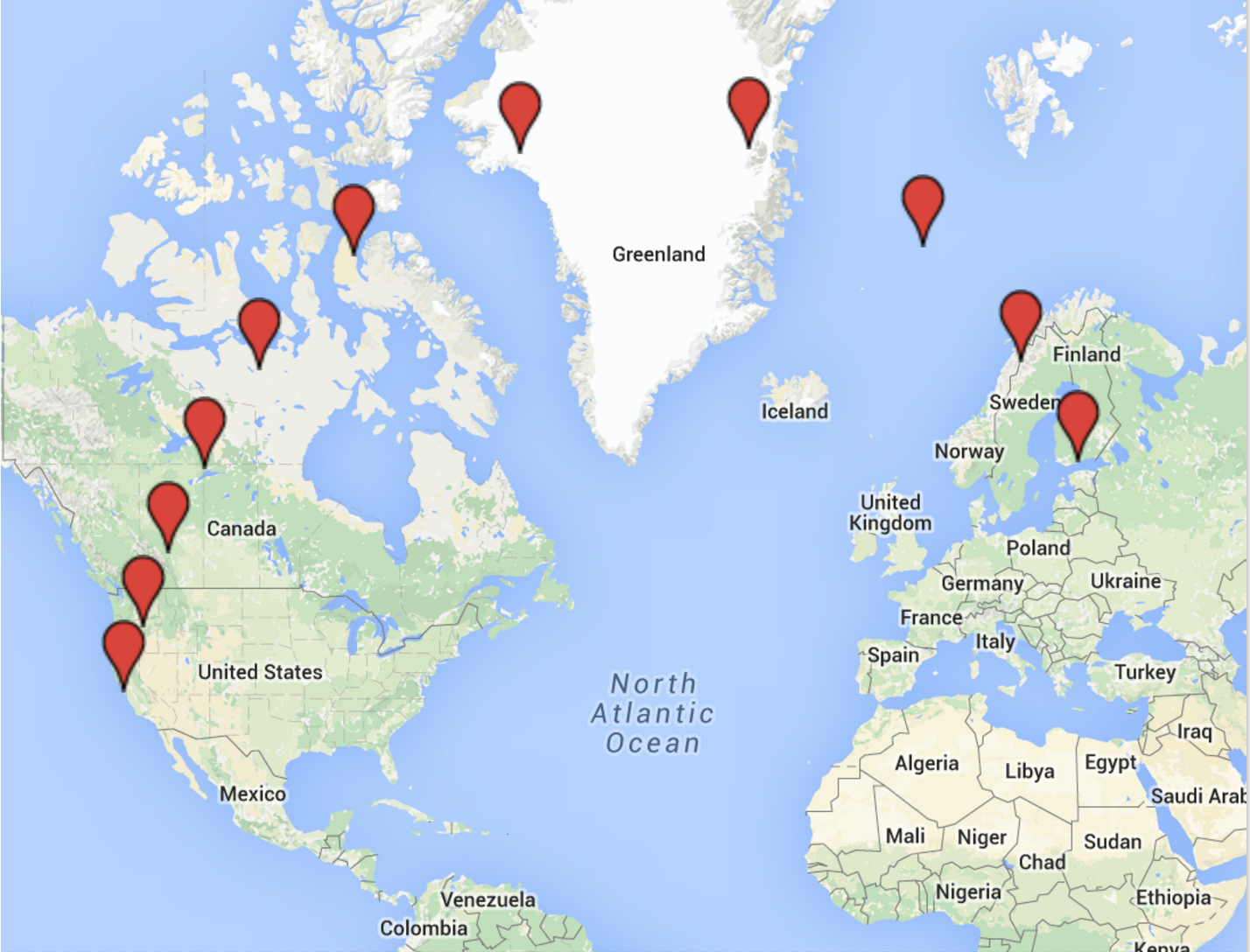
import axle.algebra.GeoCoordinates.geoCoordinatesLengthSpace

Use it to compute the points at 10% increments from SFO to HEL

val midpoints = (0 to 10).map(i => geoCoordinatesLengthSpace.onPath(sfo, hel, i / 10d))
midpoints.map(_.show)
// res25: IndexedSeq[String] = Vector(
//   "37.618900000000004° N 122.37500000000003° W",
//   "45.13070460867812° N 119.34966960499106° W",
//   "52.538395227224065° N 115.40855064022753° W",
//   "59.76229827032038° N 109.88311454897514° W",
//   "66.62843399359917° N 101.39331801935985° W",
//   "72.70253233457194° N 86.91316673834633° W",
//   "76.8357649372965° N 61.093630209243706° W",
//   "77.01752181288721° N 25.892878424459116° W",
//   "73.11964173748505° N -0.9862308621078928° W",
//   "67.1423066577233° N -16.143753987066464° W",
//   "60.3172° N -24.9633° W"
// )

SFO to HEL

Future Work